Claim:
Given any five points on a sphere, show that some four of them must lie on a closed hemisphere.

---

Intuition

When I first saw this problem, I decided to simplify it — instead of thinking about a 3D sphere, I imagined a circle in 2D.
On a circle, if you pick any five points, can you always find a semicircle that contains four of them?
That question hints at using the pigeonhole principle, and it turns out the same idea extends beautifully to the sphere.

---

Step 1: From Two Points to a Great Circle

Any two distinct points on a sphere and the center of the sphere determine a unique plane, because three non-collinear points always do.
This plane slices the sphere in a great circle — a circle whose center coincides with the sphere’s center.

---

Step 2: Two Closed Hemispheres

That great circle divides the sphere into two equal halves, each called a hemisphere.
If we include the great circle itself as part of each half, we call them closed hemispheres.

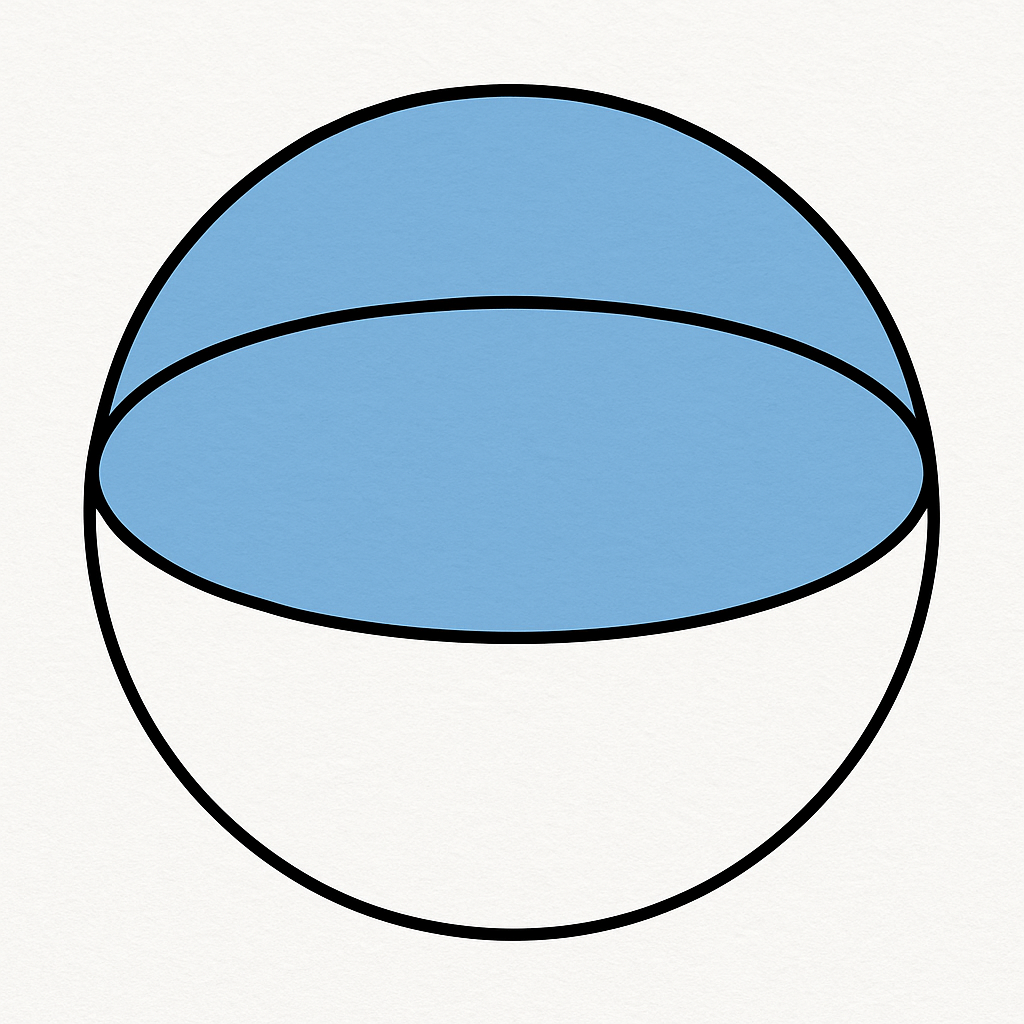
By definition, the two points we started with lie on the boundary (the great circle) of both hemispheres.

---

Step 3: The Pigeonhole Principle in Action

Now, we have three remaining points and two hemispheres.
According to the pigeonhole principle, at least one hemisphere must contain at least two of those three points.

That gives us four points — the two boundary points and the two interior ones — all lying in a single closed hemisphere.

---

Step 4: Why “Closed” Matters

If we used open hemispheres (not including the boundary), those two initial points on the great circle would belong to neither side.
By using closed hemispheres, we make sure they’re included in both, ensuring the argument holds.

---

Step 5: General Idea

This is a great example of how geometric reasoning and combinatorial thinking (like the pigeonhole principle) complement each other.
The same reasoning extends to higher dimensions: on an n-sphere, among any n + 2 points, some n + 1 must lie in a closed hemisphere.