Extracting Topology from Data: A Persistent Homology Study with the Iris Dataset
Introduction: Context and Motivation
In Summer 2024, I had the opportunity to work under Dr. Roberts on a research project exploring topological data analysis (TDA). Our aim was to understand how tools from algebraic topology—particularly persistent homology—could extract meaningful patterns from data. This project, applied to the well-known Iris dataset, allowed me to explore the rich interplay between data science and pure mathematics, laying a foundation for future research in representation theory and mathematical physics.
What is Topological Data Analysis?
Topological data analysis studies the shape of data using concepts from topology. One of the central tools is persistent homology, which tracks topological features such as connected components, loops, and voids as we vary a scale parameter.
To visualize this, we consider each data point as the center of a growing ball. As the balls expand, they begin to intersect, forming higher-dimensional shapes called simplicial complexes. Persistent homology records the birth and death of features like clusters or loops in a persistence diagram, which plots their lifespan across scales.
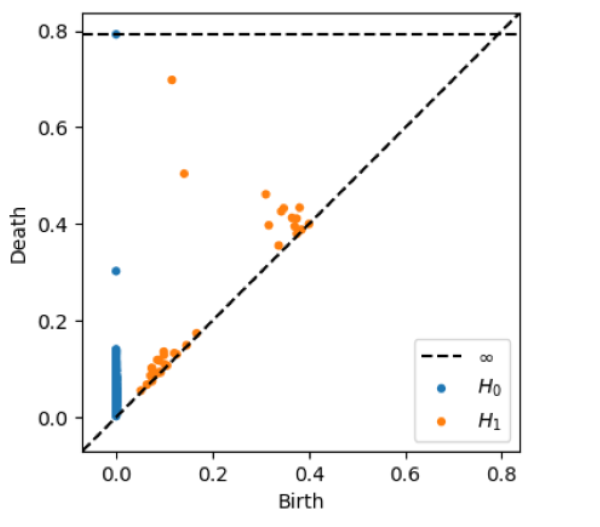
Figure: A clean H₁ loop emerges clearly in the persistence diagram from noisy circular data.
Computational Pipeline
We used the Iris dataset, a classic dataset in machine learning, to apply these ideas in practice. Using Python and the scikit-tda library suite, we:
- Imported the dataset and explored it visually.
- Experimented with both PCA-reduced data and manually selected features like petal width and length to construct point clouds. -Computed persistent homology using Ripser
- Visualized persistence diagrams using Persim and matplotlib.
1. Dimensionality Reduction with PCA
We first applied Principal Component Analysis (PCA) to reduce the 4D Iris dataset to 2D, enabling easier visualization and more efficient topological computation.
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X) 2. Computing Persistent Homology
We used Ripser, a fast and efficient library for computing persistent homology.
from ripser import ripser
diagrams = ripser(X_reduced)['dgms']3. Visualizing Persistence Diagrams
We plotted the resulting diagrams to observe the lifespan of 0-dimensional (connected components) and 1-dimensional (loops) features.
from persim import plot_diagrams
plot_diagrams(diagrams, show=True)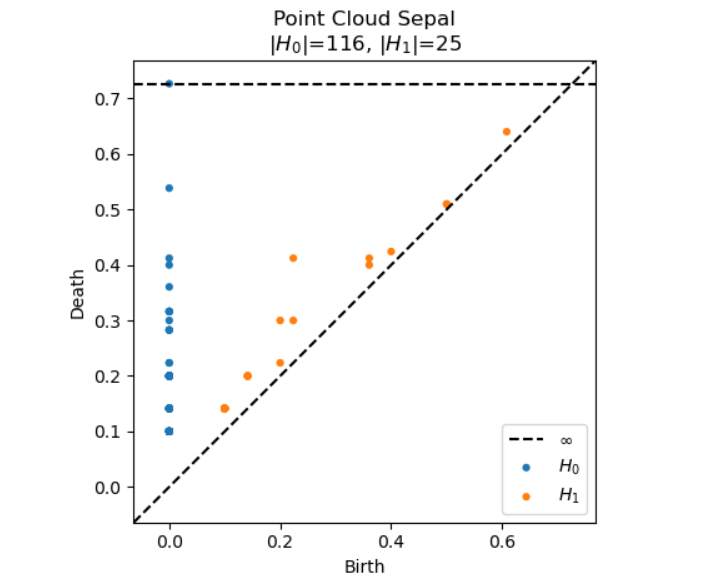
Figure: Persistence diagram computed from PCA-reduced Iris dataset. to observe the lifespan of 0-dimensional (connected components) and 1-dimensional (loops) features.
While the diagrams did not yield definitive conclusions about the structure of the Iris dataset, this computational pipeline was a vital part of my learning process. It helped me solidify the mechanics of persistent homology, develop familiarity with key tools in the TDA ecosystem, and appreciate the subtle challenges of interpreting topological summaries of real-world data.
What We Learned From the Process
Although we did not reach definitive analytical conclusions using the Iris dataset, the process of building this pipeline taught me a great deal. The exploratory approach—testing code, generating persistence diagrams, and interpreting features—helped me internalize the logic of TDA. Even without clean-cut results, I gained valuable experience with tools like Ripser and Persim, and deepened my appreciation for how algebraic topology can inform data-driven work.
Reflections and Learnings
Although we had limited time to explore deeper variations or extended datasets, this project introduced me to the power of topological methods in understanding structure in data. I gained practical experience in using Python libraries for topological data analysis, and developed a better appreciation for how concepts like Betti numbers and simplicial complexes manifest computationally.
Broader Research Fit
This experience deepened my interest in the intersection of pure mathematics and computation. I am particularly drawn to how tools from topology and algebra can be brought into data analysis, machine learning, and even mathematical physics.
As I look ahead to graduate research, I am eager to explore connections between persistent homology, symmetry, and representation theory. The potential of combining abstract structures with real-world data inspires my future path in mathematics.
Feel free to reach out or leave a comment if you’re also interested in topological data analysis or are working on similar projects!