One-Dimensional Dynamical Systems

Introduction

Have you ever wondered how mathematicians predict the behavior of systems over time without solving complicated equations?
In my recent studies of dynamical systems, I discovered an elegant geometric approach that transforms differential equations into visual, intuitive flows. Let me share what I learned about one-dimensional systems and why they’re the perfect starting point for understanding dynamics.

What Are First-Order Systems?

A first-order (or one-dimensional) system is simply an equation of the form:

Here, represents some quantity that changes over time , and is a smooth function that tells us the rate of change.
The dot notation () means the derivative with respect to time.

These systems are called autonomous because they don’t depend explicitly on time—the rate of change at any point depends only on where you are, not when you are there.

The Power of Pictures Over Formulas

One of the most eye-opening lessons from this topic was that pictures often outperform formulas when analyzing nonlinear systems.

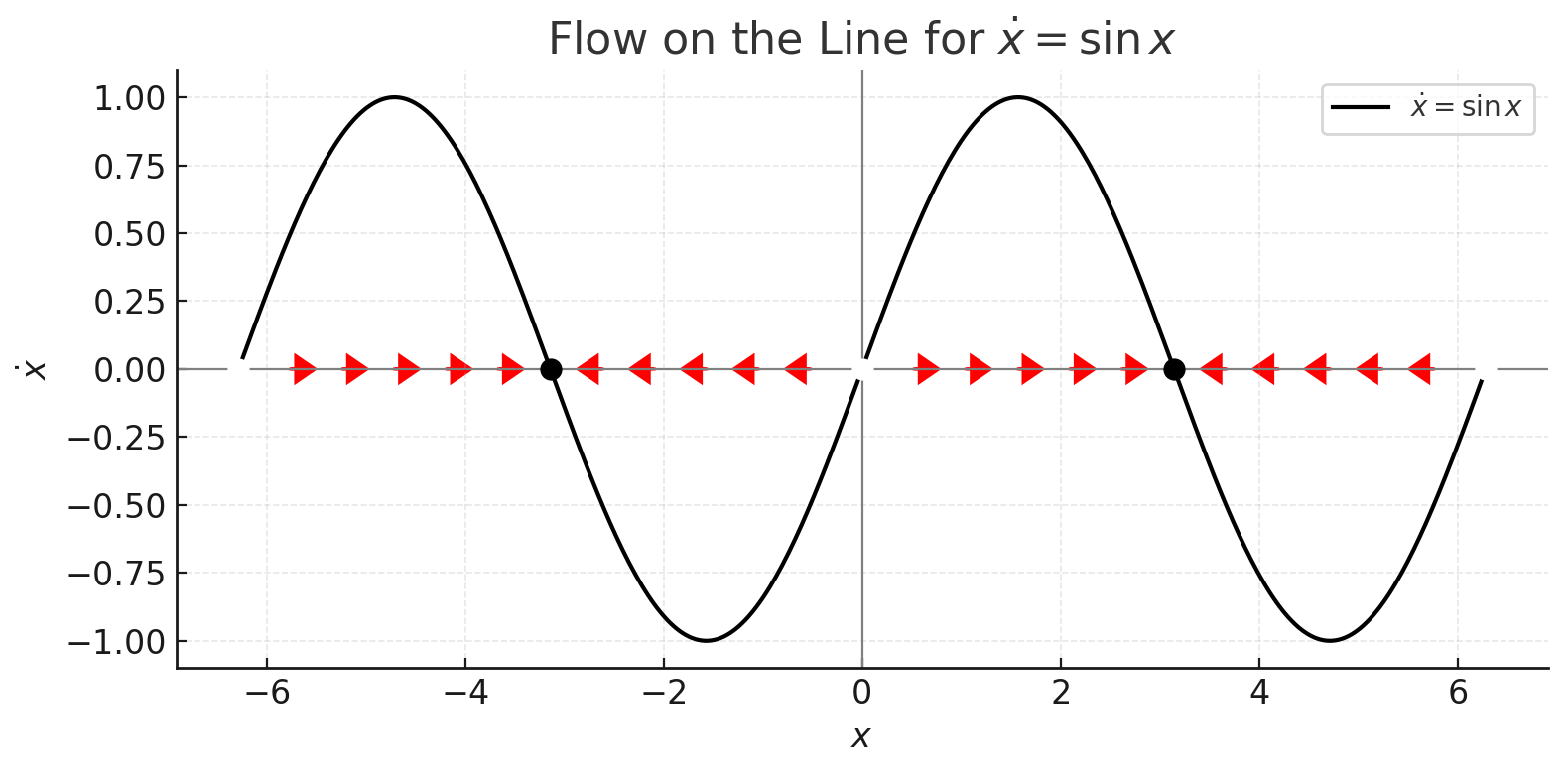
Consider the equation . While this can be solved analytically (yielding a messy logarithmic expression), the geometric approach is far more illuminating. Instead of wrestling with formulas, we can:

  1. Plot versus
  2. Draw arrows on the x-axis showing the direction and speed of flow
  3. Immediately see where the system is heading

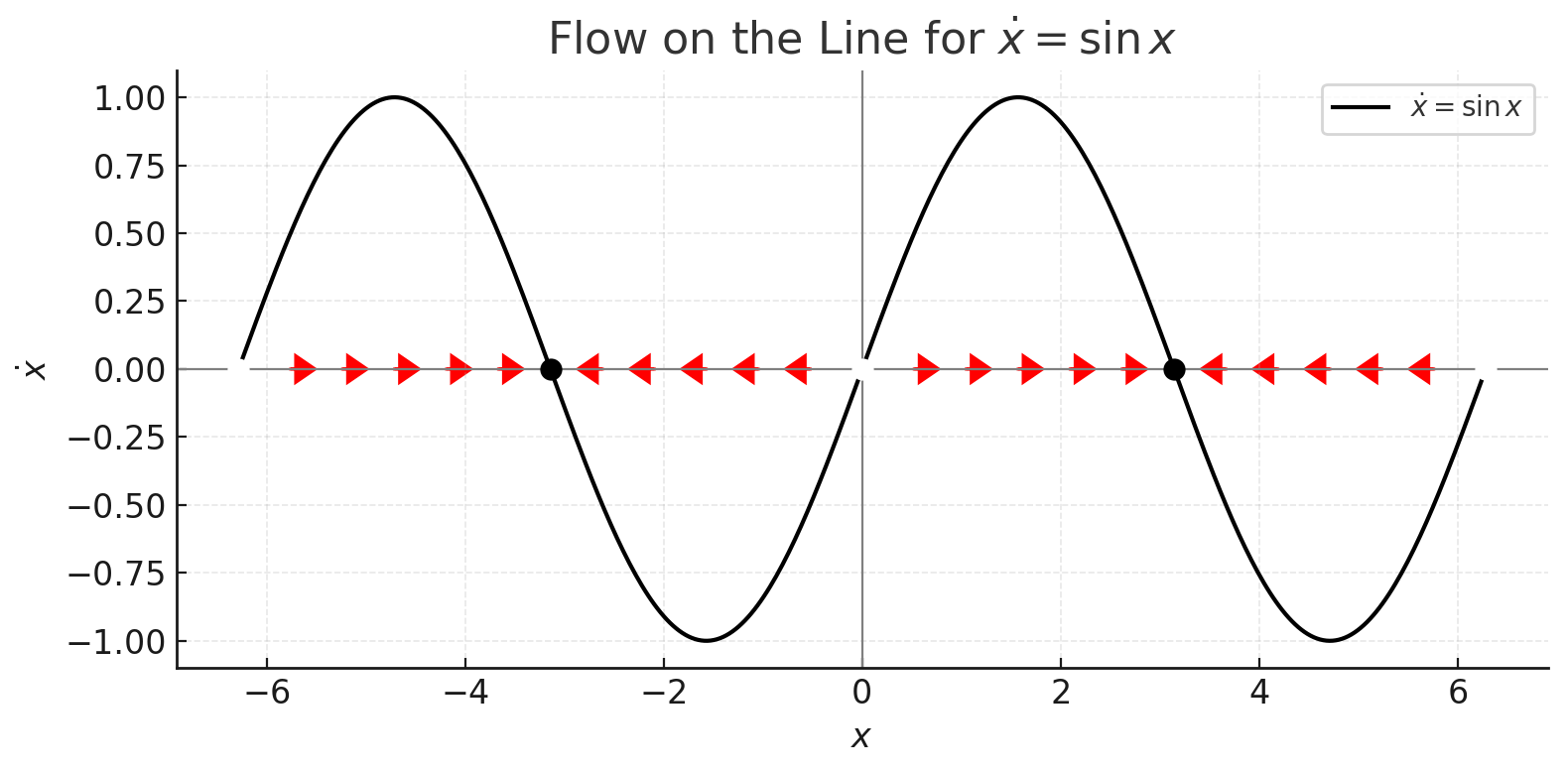
Flow on the line

This visual approach reveals the system’s behavior at a glance, answering questions like “what happens as ?” without any calculation.

The Vector Field Interpretation

Here’s the key insight: think of the differential equation as describing fluid flow along a line.

Imagine a river flowing along the real number line, where:

  • The velocity at each point is given by
  • Flow moves right when
  • Flow moves left when
  • Flow stops at points where

These stopping points are called fixed points or equilibrium points, and they’re the stars of the show in one-dimensional dynamics.

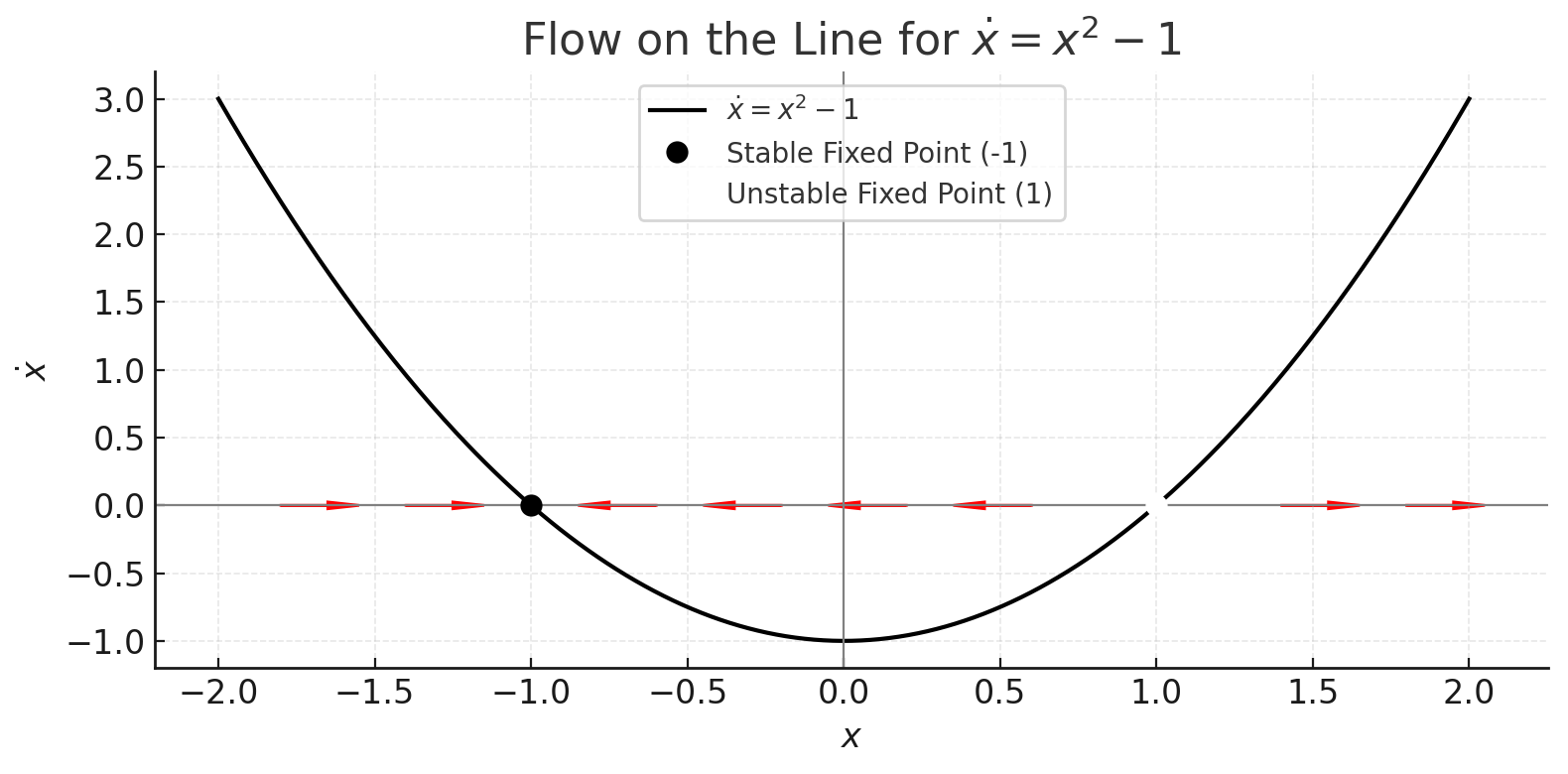
Fixed Points and Stability

Fixed points come in two flavors:

Stable Fixed Points (Attractors/Sinks)

  • Represented by solid black dots
  • The flow moves toward them from nearby points
  • Small disturbances decay over time
  • Think of a marble settling at the bottom of a bowl

Unstable Fixed Points (Repellers/Sources)

  • Represented by open circles
  • The flow moves away from them
  • Small disturbances grow over time
  • Think of a marble balanced on top of a hill

There’s also a rare third type called half-stable fixed points, which attract from one side and repel from the other.

Logistic Growth

A Real-World Example: The Logistic Equation

One of the most important applications is modeling population growth.
The simple exponential model predicts unlimited growth, which is unrealistic. The logistic equation improves this:

Where:

  • : population size
  • : growth rate
  • : carrying capacity (maximum sustainable population)

This model has two fixed points:

  • → unstable (extinction is precarious)
  • → stable (populations naturally approach carrying capacity)

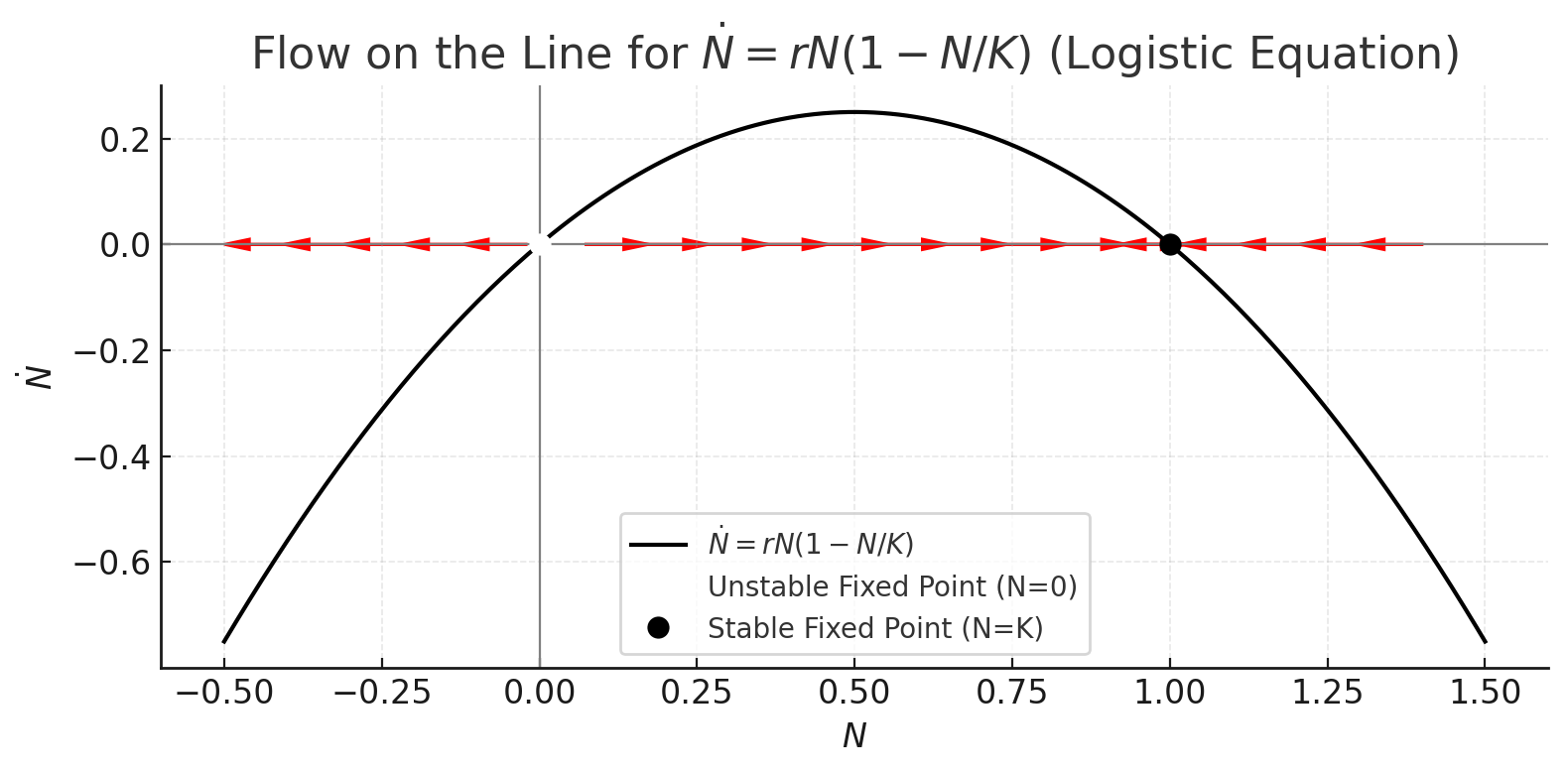
Logistic Equation

The phase portrait reveals that populations below grow in an S-shaped (sigmoid) curve, while populations above decline back down.
This captures the real-world behavior of resource-limited populations far better than exponential models.

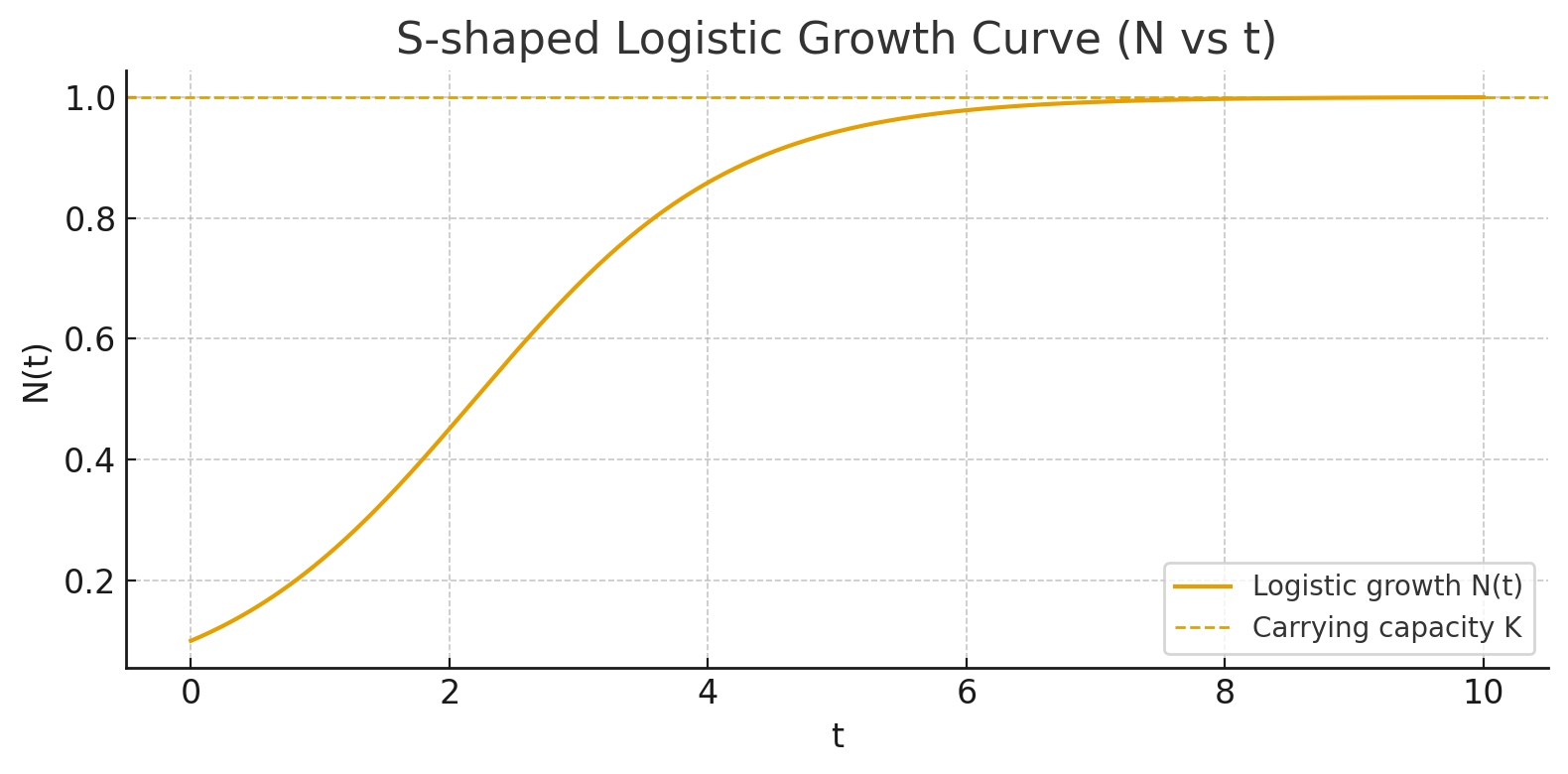
Logistic Growth

How the Two Graphs Are Connected

The parabolic plot of vs. and the S-shaped curve of vs. describe the same process from two complementary perspectives.

In the first graph, shows how the rate of growth depends on the current population:

When is small, is small but positive — the population grows slowly.

Around , reaches its maximum — growth is fastest.

As approaches , decreases back to zero — growth slows down.

Now, if you follow this flow along the line and integrate it through time, you get the S-shaped logistic curve . It starts nearly flat (slow growth), rises steeply in the middle (fast growth), and then flattens again near the carrying capacity.

In short:

The flow on the line explains why the logistic curve bends the way it does.

The S-shape is the time-domain result of moving along that parabolic flow field.

Linear Stability Analysis

While geometric methods are intuitive, we sometimes need quantitative measures of stability.
That’s where linear stability analysis comes in.

For a fixed point , we check the slope :

  • If : stable fixed point
  • If : unstable fixed point
  • If : indeterminate (requires nonlinear analysis)

The magnitude tells us the rate of approach or departure.
Its reciprocal gives a characteristic timescale for the dynamics near that fixed point.

A Fundamental Limitation: No Oscillations

Here’s a surprising fact: first-order systems cannot oscillate.

Solutions either:

  • Approach a fixed point monotonically
  • Diverge to infinity
  • Remain constant

This is fundamentally topological.
When you flow along a line, you can only move in one direction (or stay still).
You can never return to where you started, so periodic solutions are impossible.

The mechanical analog makes this obvious: imagine a mass in viscous fluid (like honey) attached to a spring.
With enormous damping and negligible inertia, the mass slowly creeps toward equilibrium without any overshoot or oscillation.

The Potential Energy Perspective

There’s an elegant alternative visualization using potential energy.
Define a potential such that:

Now the dynamics can be pictured as a heavily damped particle sliding down the walls of a potential well.
The particle always moves “downhill” toward lower potential:

  • Local minima of → stable fixed points
  • Local maxima of → unstable fixed points

This perspective is particularly useful in physics and can be extended to more complex systems.

Key Takeaways

  1. Geometric thinking beats algebraic manipulation for understanding nonlinear systems
  2. Fixed points dominate the dynamics of first-order systems
  3. Visual phase portraits reveal qualitative behavior instantly
  4. First-order systems are fundamentally simple — no oscillations, no chaos
  5. Multiple perspectives (vector fields, potentials, mechanical analogs) deepen understanding

Looking Ahead

One-dimensional systems are just the beginning.
While they can’t oscillate or exhibit chaos, they provide the essential toolkit for analyzing more complex systems.
The concepts of fixed points, stability, phase portraits, and linearization extend naturally to higher dimensions, where the real excitement begins.

But before tackling those complexities, mastering flows on the line gives you an intuitive foundation that makes everything else easier to understand.

This post summarizes concepts from a course in nonlinear dynamics and chaos, drawing inspiration from Steven H. Strogatz’s Nonlinear Dynamics and Chaos (1994). If you’re interested in learning more, I highly recommend working through similar exercises and experimenting with dynamical systems software to build intuition.