This semester, I immersed myself in topology for the first time—and one of the most fascinating, mind-bending concepts I encountered was the Cantor set. What began as a seemingly simple construction—repeatedly removing the middle third from an interval—quickly unfolded into a set so rich with mathematical depth that it fundamentally changed the way I think about structure, continuity, and infinity.

What is the Cantor Set?

The Cantor set is constructed from the closed interval $[0, 1]$ by removing the open middle third $(1/3, 2/3)$. Then, from the remaining two intervals $[0, 1/3]$ and $[2/3, 1]$, we again remove the open middle third from each, and continue this process ad infinitum.

Despite being created by deleting intervals repeatedly, the resulting set:

• Contains uncountably infinitely many points
• Has measure zero (takes up no “length”)
• Is closed, perfect, and totally disconnected

Here’s a visual representation of its construction up to 5 levels:

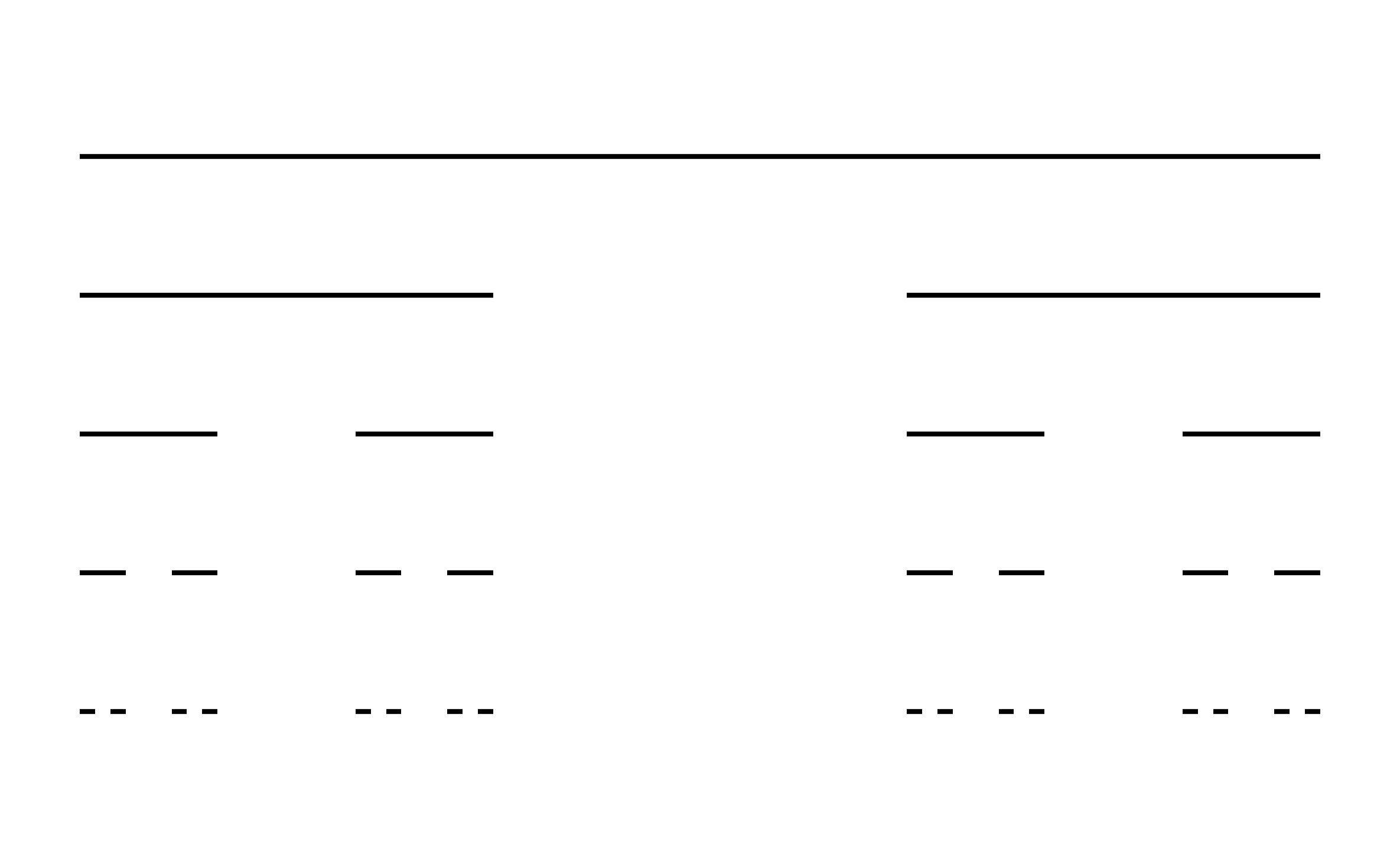
Each horizontal line above shows the remaining intervals after each iteration. Notice how quickly the set becomes fragmented—and yet, incredibly, an uncountable number of points remain.

Why It Shocked Me

Early in the semester, I found myself clinging to intuition rooted in geometry and calculus. But the Cantor set shattered those instincts:

• How can a set be nowhere dense but still uncountable?
• How can it contain no intervals, yet be perfect (every point is a limit point)?
• How can its total length shrink to zero, yet never fully disappear?

Theorems That Changed My Perspective

Theorem: The Lebesgue measure of the Cantor set is 0.

This follows from the geometric series:

Theorem: The Cantor set is uncountable.

This is often proven by constructing a bijection between the Cantor set and the set of all infinite binary sequences—hinting at deep connections with set theory and symbolic dynamics.

The Cantor Set and My Growth

Encountering this paradoxical object taught me something about math and about myself:

1. Mathematics isn’t about confirming intuition—it’s about building new ones.
2. I saw firsthand how rigor and abstraction can clarify, rather than obscure, our understanding.
3. I learned to think in terms of structures and properties rather than pictures alone.

One of the most profound concepts I encountered in this course was compactness. Initially abstract, I slowly began to see its power. The Cantor set, despite being so fragmented, is compact—it is both closed and bounded.

A Compactness Example That Clicked for Me

I later came across an informal visualization that really resonated with me: imagine a tiny ant crawling around on a shape. If the space is compact, no matter how the ant moves, it can’t “escape” to infinity—there’s always a limit point, always a place it will cluster around. It helped me understand why compactness is so central in analysis: it ensures that functions behave well, sequences converge, and mathematical chaos has boundaries.

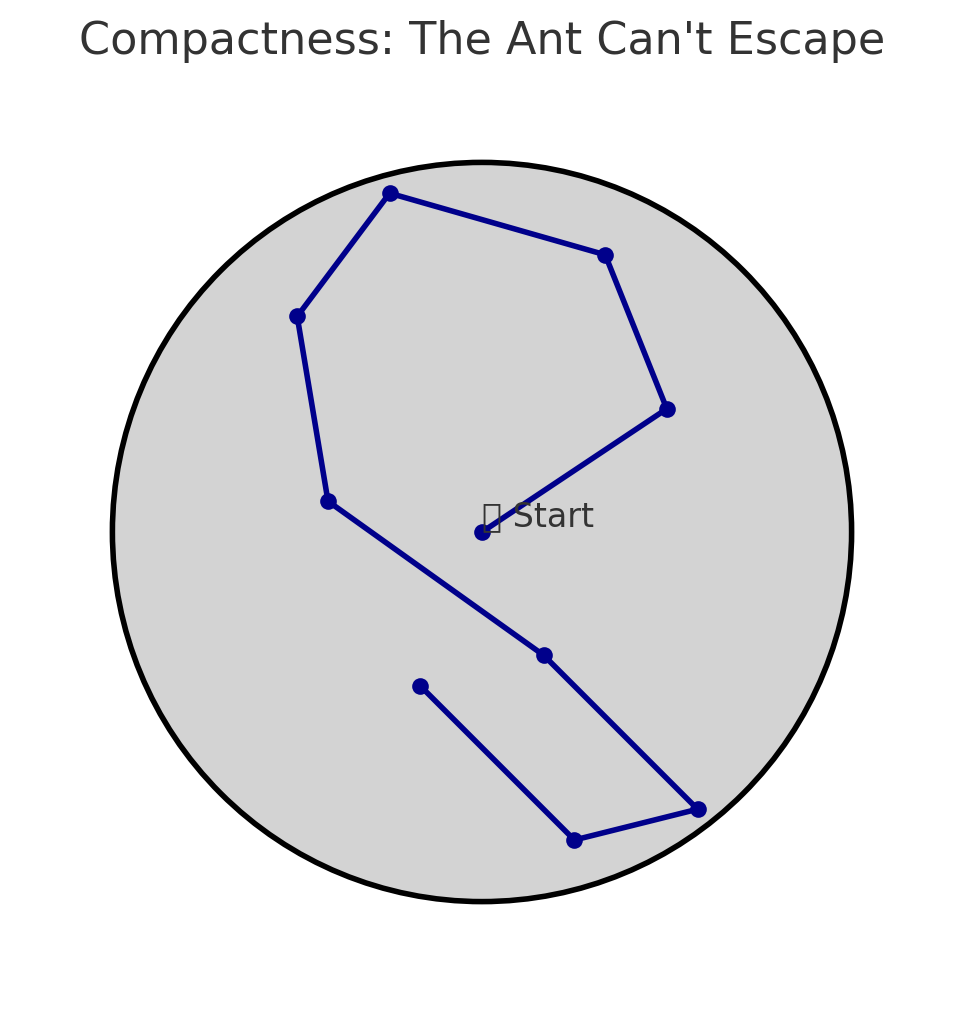
In this illustration, the circle represents a compact space. The ant, wandering around, is always contained—showing that compactness ensures the presence of limit points and prevents escape to infinity.

A Bit of Code for Fun 🐍

Here’s a simple Python script that draws the Cantor set using recursion:

import matplotlib.pyplot as plt

def cantor_set(ax, x, y, length, depth):
    if depth == 0:
        ax.hlines(y, x, x + length, colors='black', linewidth=2)
    else:
        third = length / 3
        cantor_set(ax, x, y, third, depth - 1)
        cantor_set(ax, x + 2 * third, y, third, depth - 1)

fig, ax = plt.subplots(figsize=(8, 5))
ax.set_title("Construction of the Cantor Set (up to 5 levels)")
ax.set_xlim(0, 1)
ax.set_ylim(-0.5, 5.5)
ax.axis('off')

for i in range(6):
    cantor_set(ax, 0, i, 1, i)

plt.tight_layout()
plt.show() 

Looking Forward

As I prepare to apply for PhD programs in pure mathematics, I realize this class didn’t just teach me topology—it helped shape the kind of mathematician I want to be. I want to keep asking questions that surprise me. I want to live in the tension between intuition and rigor. I want to contribute to conversations that explore the limits of mathematical understanding.

The Cantor set was a humbling and inspiring chapter in that journey.

Thanks for reading. If you’re also into topology, or just love math that messes with your head, feel free to reach out!